
What is GaspiLS?
GaspiLS is a scalable linear solver library for the exascale age and is industry proven in CFD and FEM simulations. Its easily extendable standard API is compact, yet powerful for parallel computations and allows for smooth transitions from legacy applications in little to no time.
GaspiLS comes with a collection of iterative solvers (Richardson, (P)CG, BiPCGStab, GMRES) and preconditiones (Jacobi, ILU(0), MILU), which can be easily expanded by adding custom solvers and/or preconditioners.
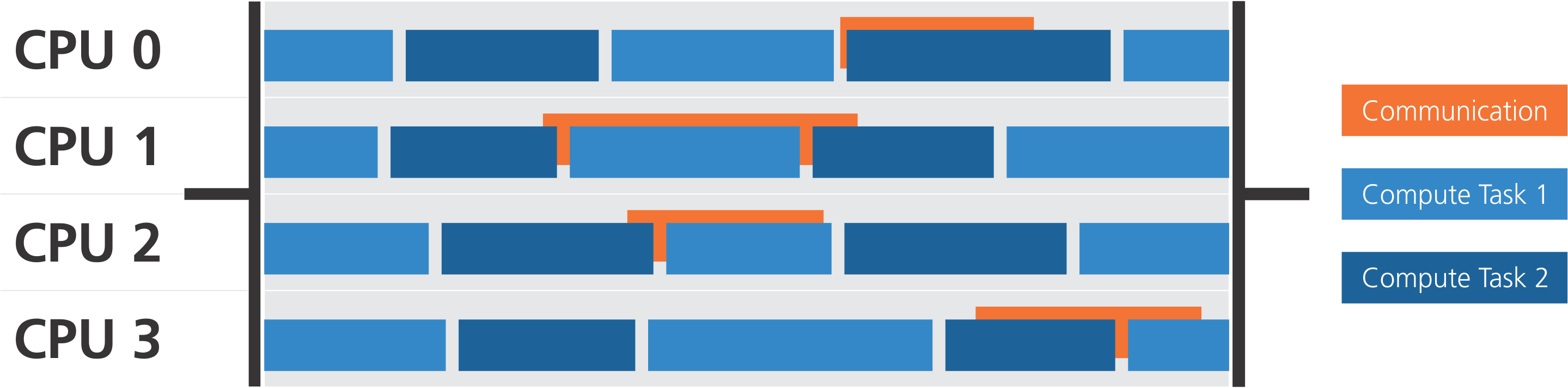
A hybrid-parallel implementation for scalability results in a much better surface to volume ratio and the task based parallelization yields optimal load balancing. The design is multi-threaded with thread-safe matrix assembly and fully threaded matrix finalization.
GaspiLS inherits the Gaspi/GPI-2 programming model and leverages its unique advantages to achieve overlap of computation and communication.
GaspiLS is open-source GPLv3. Download and try it out now!
State of the art preconditioners
Preconditioners are designed to improve the convergence of iterative Krylov subspace solvers, i.e. they reduce the number of required iterations or are even a necessary condition to solve a given problem at all. Therefore, beside the asolute performance and scalability of the basic solvers provided by GapiLS, preconditioners are a key component to solve sparse linear systems efficiently.
GaspiLS provides two classes of black-box preconditioners, now. Algebraic Multigrid (AMG) for symmetric positive definite problems as they appear e.g. in CFD applications and Multi-Level ILU factorizations as a generic preconditioner. Both implementations follow a scalable, efficient, hybrid parallel Gaspi based approach.
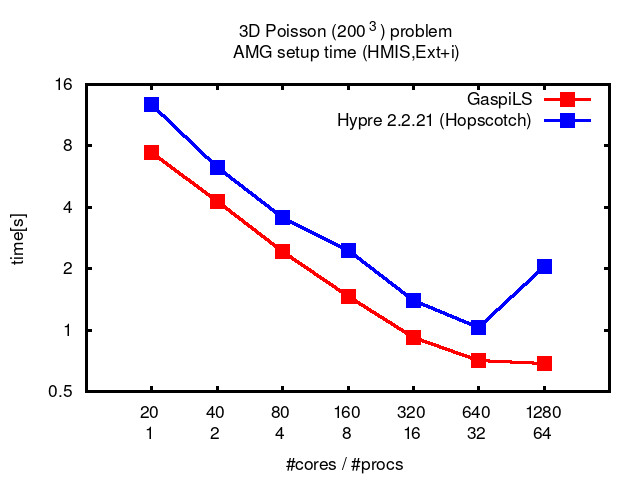
AMG, as representative of a multigrid method, has a linear computational complexity, which is optimal. It can be applied to symmetric positive definite problems. In AMG, a hierarchy of operators is directly constructed from the linear system, without explicit knowledge of the underlying geometry or partial differential equation.
GaspiLS provides better scalability and performance than hypre.
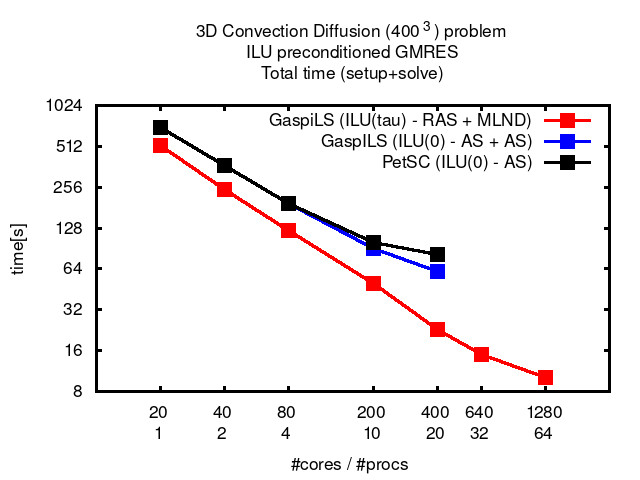
Multi-Level ILU, on the other hand, is widely used because of its robustness, accuracy, and usability as a black-box preconditioner for general sparse linear systems. ILU consists of LU based Gaussian elimination combined with dropping. Depending on the chosen input parameters and the amount of available resources, Multi-Level ILU allows for seamless interpolation between full Gaussian elimination on one end (exact inverse, high resource consumption) and Jacobi preconditioning on the other end (low resource consumption, low quality).
GaspiLS provides a whole ILU preconditioner toolbox. Different preconditioners are possible based on the following building blocks:
- Partial Incomplete Crout LU Factorization
- Inverse based pivoting, deferral, dropping
- Multi-Leveling
- Domain Decomposition methods
–> GaspiLS ILU preconditioners are generic, robust, stable and scalable
Performance & Scalability
The need for scalability is driven by the hardware trend of increased parallelism.
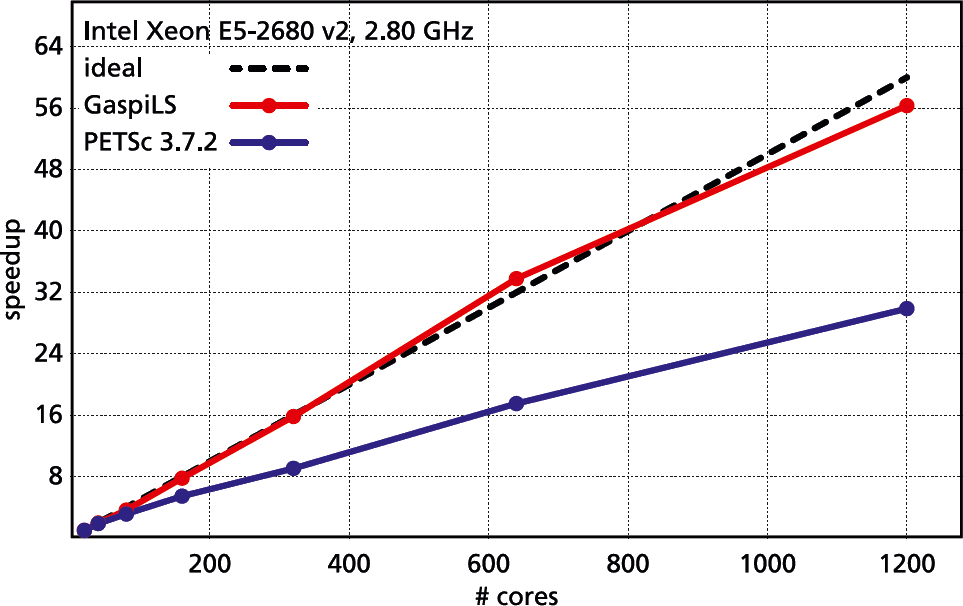
Scalability quantifies the additional benefit generated by adding extra resources to a computational problem. In case of optimal scalability, this benefit is 100 percent and only optimal scalability can guarantee full resource utilization. GaspiLS delivers superior performance and scalability, which means:
- Time to solution can be practically reduced as much as required by adding extra resources.
- There is pratically no limit on the modelling complexity and its enormous memory footprint, as memory is simply accumulated across nodes.
- There is no need for expensive resources. Instead of high-end fat nodes, use a bunch of cheap commodity hardware nodes.
- Optimal energy efficiency because hardware is used to capacity and never sits around being idle.
Advantages
GaspiLS achieves its superior scalability and performance by striving for 100 percent resource utilization.
Testimonials
Don't take it from us, take it from those who are using GaspiLS already.

GaspiLS has received funding from the European Union’s Horizon 2020 research and innovation programme in the scope of the HYSCALA project under the grant agreement No 800881.


